The Graph of a Rational Function Sometimes Has a Hole

By Bio_Lauren300 12 May, 2022 Post a Comment

Choose the correct answer below. To account for this I leave a nice big open circle at the point.

Rational Function Holes Explanation And Examples

F 2 3.

. So if you draw the graph of this rational comes in you can see that the value of X very busy was is not in the looming so blooming off. For factors in the numerator not common to the denominator determine where each factor of the numerator is zero to find the x x -intercepts. Decide whether the following statement is true or false.

This is thanks belonging to our developed off ex accept exes. After crossing out the common factors at both numerator and denominator in the given rational function we get. Hence the graph of rational function sometimes have hole.

For example the function may be re-written by factoring the numerator and the denominator. The graph of a rational function sometimes has a hole. Given that it is only sometimes and not all the time it is true that the graph of a rational function sometimes has a hole.

It shows that this point is not present on the graph of the rational function. Evaluate the function at 0 to find the y -intercept. This occurs when there is a common factor in the numerator and denominator.

Nothing will do so its not important. Cancel the factor in the expression for x2-5x f x x-r-46. How to find them and the two different possibilities for graphing these strange functions.

This would be equal to X minus one upon X plus you. F x x 1 ------ 1 If we substitute 2 for x we get get. We have step-by-step solutions for your textbooks written by Bartleby experts.

Who says that the value off the function at this. Instead you find the slant asymptote equation in this case y x 1 and you draw that in for the rational graph. The graph of a rational function sometimes has a hole.

O True O False. Laminiaduo7 and 5 more users found this answer helpful. Eq Choose the correct graph for the rational.

Fortunately the effect on the shape of the graph at those. Notice that is a common factor to the numerator and the denominator. Um and heres a situation where this is true.

Nothing will do so its not important. Um that means that theres a whole at that point in the graph and so therefore yes it is true that some graphs can have so are some graphs can have holds some rational functions can have holes. The graph of the function f x3x4-x35x2-2x-7 will behave like the graph of ______ for larger values of x.

Consider a rational function in the form of p q where q 0 has some factors which are easily divisible by the numerator value. As with polynomials factors of the numerator may have integer powers greater than one. Factor the numerator and denominator.

The graph of a rational function sometimes has a hole. Check whether given statement is true or false. The graph of a rational function usually has vertical asymptotes where the denominator equals 0.

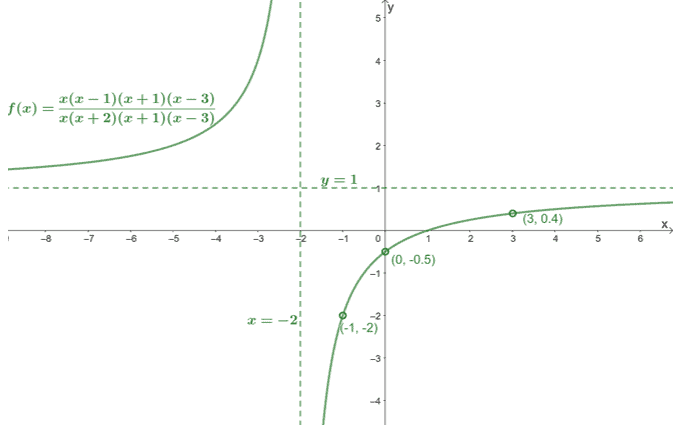
The only difference between the slant asymptote of the rational function and the rational function itself is that the rational function isnt defined at x 2. So the hole will appear on the graph at the point 2 3. The domain of every rational function is the set of all real numbers.

Occasionally a graph will contain a hole. In Example 9 we see that the numerator of a rational function reveals the x -intercepts of the graph whereas the denominator reveals the vertical asymptotes of the graph. EqF x dfrac x2 - x -6 x-3.

So there is a hole at. Factor the rational function. The graph of a rational function may intersect a horizontal asymptote.

O True O False. If as x approaches some number c the values of Rx - infinity then the line x c is a _____ asymptote of the graph of R. And theres no assemble at X equals who So the graph of the function out of excellent have a whole X equals two who that the value of the country is not keeping.

HOLES in rational functions. The graph of a rational function sometimes has a hole. Graphing a Rational Function with Holes Precalculus Skills Practice Plot the given rational function.

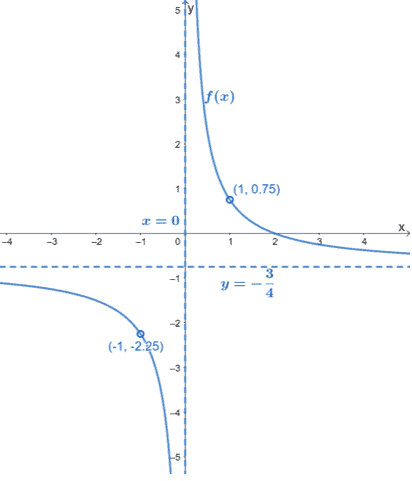
The holes in a rational function are the result of it sharing common factors shared by the numerator and denominator. For example the rational function y 4 x 2 x 2 x 2 x has a hole at x 0. These are coordinates that the function passes through but are not part of the functions domain and range.

Expert Answer Transcribed image text. Choose the correct answer below. However the graph of a rational function will have a hole when a value of x causes both the numerator and the denominator to equal 0.

We call such a hole a removable discontinuity. Decide whether the following statement is true or false. Who says that the value off the function at this particular point will not vilifying.

For a rational function R if the degree of the numerator is less than the degree of the denominator then R is ____. The correct answer for the given statement above would be TRUE. This is thanks belonging to our developed off ex accept exes.

Fx ax-h2 k. Holes in the Graph of a Rational Function Sometimes the numerator and the denominator of a rational function are both zero at the same time. Please note that the graphs of the rational functions satisfy the vertical line test.

Hope this is the answer that you are looking for. Identify the common factors on the numerator and denominator. Steps to Graph a Rational Function with Holes Step 1.

In this case the zero in the denominator need not cause the graph to have a vertical asymptote. Find the multiplicities of the x x -intercepts to determine. Up to 10 cash back This excluded value is usually referred to as hole in the rational function.

Given a rational function sketch a graph. A single point where the graph is not defined indicated by an open circle. The hole of the rational function is x 3.

When a function contains holes we actually need them as guide points when graphing the functions curve.

Rational Function Holes Explanation And Examples